图像处理编程作业
图像处理实验报告
一、实验一
1、验证去雾算法
实验使用的去雾算法是何凯明发表在CVPR2009年《Single Image Haze Removal Using Dark Channel Prior》的论文。文章主要基于暗通道先验来进行带雾图像的还原。
-
首先,在计算机视觉和计算机图形中,下述方程所描述的雾图形成模型被广泛使用:
表示输入的图像,表示要还原的图像,表示全球大气光成分,表示透射率, 因此我们的目标就是要估计和。
-
这里使用的就是暗通道进行估计和。实际上,这是一个统计规律。暗通道就是取三通道中三者的最小值
-
然后使用暗通道中前0.1%亮的像素对应的原图像素的最大值(实现中使用了平均值)作为的估计。对于的估计,使用了以下式子。
-
最终的目标公式如下。
以下是复现了上述论文主要流程的实验结果。
| origin | processed |
|---|---|
 |
 |
| origin | processed |
|---|---|
 |
 |
| origin | processed |
|---|---|
 |
 |
| origin | processed |
|---|---|
 |
 |
分析各参数对于去雾结果的影响:
- 最小值滤波窗口大小 :最小值滤波是用于暗通道的像素提取,根据实验结果可以发现,最小值滤波的窗口大小越小,图片中黑色的区域会越明显。
| size = 5 | size = 10 | size = 15 |
|---|---|---|
 |
 |
 |
| size = 20 | size = 25 | size = 30 |
|---|---|---|
 |
 |
 |
- 控制去雾程度的参数 :正常的大气中是存在少量雾气的,也就是说在输出的图像中,也会存在少许的雾气。从实验结果可以观察到,越大,去雾程度越高。
| ω = 0.5 | ω = 0.6 | ω = 0.7 |
|---|---|---|
 |
 |
 |
| ω = 0.8 | ω = 0.9 | ω = 1.0 |
|---|---|---|
 |
 |
 |
2、彩色直方图均衡化
直方图均衡化通常用来增加许多图像的全局对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
彩色直方图均衡化,就是对于RGB三通道的图像去进行均衡化。实际上,对彩色分量rgb分别做均衡化,会产生奇异的点,图像不和谐。一般是对于YUV的V通道,Lab的L通道,HSV的V通道进行均衡化,也就是亮度通道。

由于,亮度是由不同比例的RGB进行混合计算的。因此在将RGB分别进行均衡化之后,实际上并不是按照亮度比例进行均衡化,因此图像会有失真的现象,具体表现为偏蓝紫色,因为蓝色的偏多了。YUV的亮度值就是由的公式估计的,因此对于亮度通道进行均衡化,并不会出现失真的现象。HSV的亮度值是由估计的,因此在对于亮度进行均衡化时,会出现些许的失真。Lab的亮度值与YUV一样,所以不会出现失真的现象。
3、模仿美图秀秀的功能
- 祛痘美白
我实现的祛痘美白效果的主要原理是首先对图像使用双边滤波,对图像进行一定的磨皮。然后对原图和磨皮之后的图像作差后加上128,去获取带痘的区域,将其使用高斯模糊之后,再与原图以一定的比例混合。
| origin | processed |
|---|---|
 |
 |
- 雕刻效果
雕刻效果的实现与获取带痘区域的做法类似,对比相邻的两个像素,如果他们的差值加上200大于一个255或者小于0,就让他是255或者0,这样,颜色差异明显的区域就会显示成白或者黑,其他差异不明显的就会变成灰色。
| origin | processed |
|---|---|
 |
 |
- 素描
素描的效果是使用了反相之后的灰度图,再将其使用高斯模糊处理之后反相回去,对原图对应的灰度图除上处理过后的反相图。这样子,能够比较柔和地将边缘表现出来。
| origin | processed |
|---|---|
 |
 |
- 蜡笔画
蜡笔的效果也是去提取图像的边缘,主要的方法是对原图像灰度化之后使用自适应滤波将其转为二值图后反相,边缘就会显示成白色,别的区域显示成黑色,然后原图和边缘进行与操作,就能够只保留边缘的彩色部分。
| origin | processed |
|---|---|
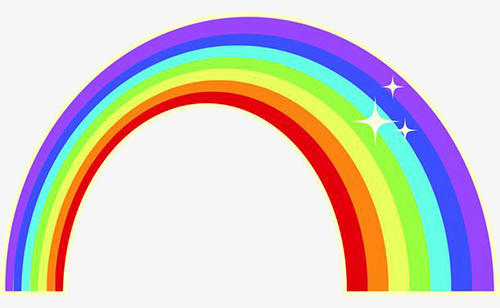 |
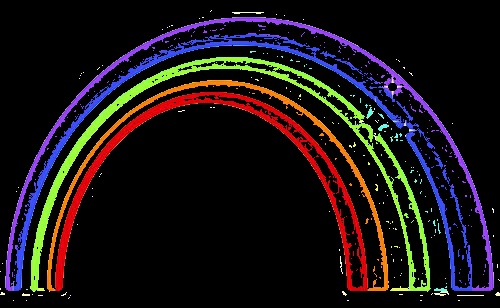 |
二、实验二
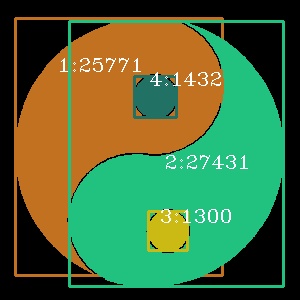
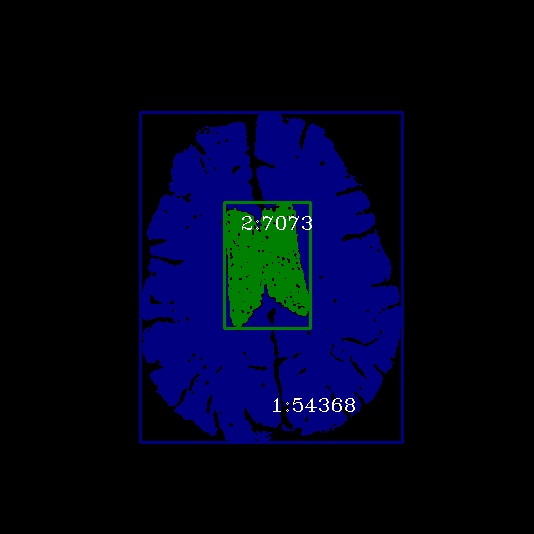
1、实现区域生长算法并进行连通标号;求每个区域的面积,外接矩形。
我所采用的区域生长算法是种子区域生长算法,首先指定不同区域的种子点,然后沿着种子点不断搜索八邻域的点,如果领域的点与种子点的像素差小于一个阈值,就认为是同一个区域,并继续搜索领域的点,如此往复。在实际操作中,我将判断一个点是否属于一个种子区域的标准改成了待判断点与该种子区域的平均像素进行比较,这样子的效果会比直接使用种子点像素比较好一些。计算每个区域的最小最大高宽,画上外接矩形,计算每个区域的像素个数,记作面积,并对每个区域标上标号。
| origin | processed |
|---|---|
 |
 |
 |
 |
 |
 |
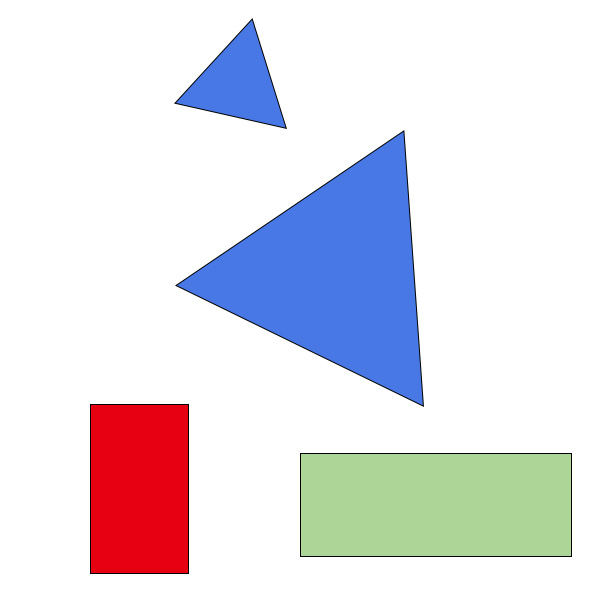
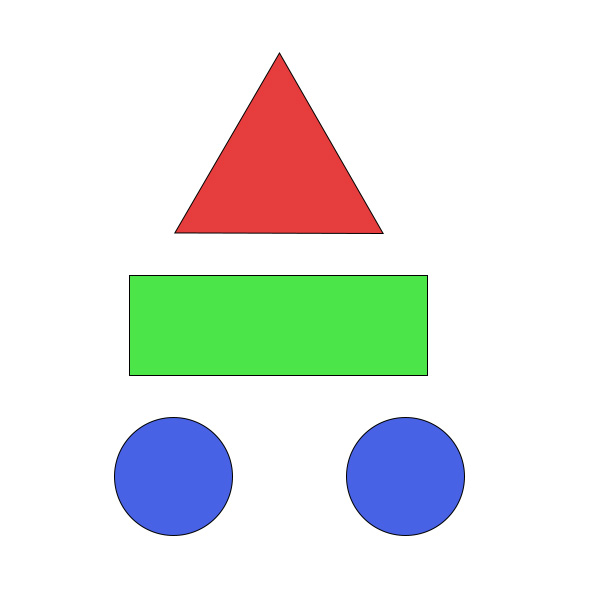
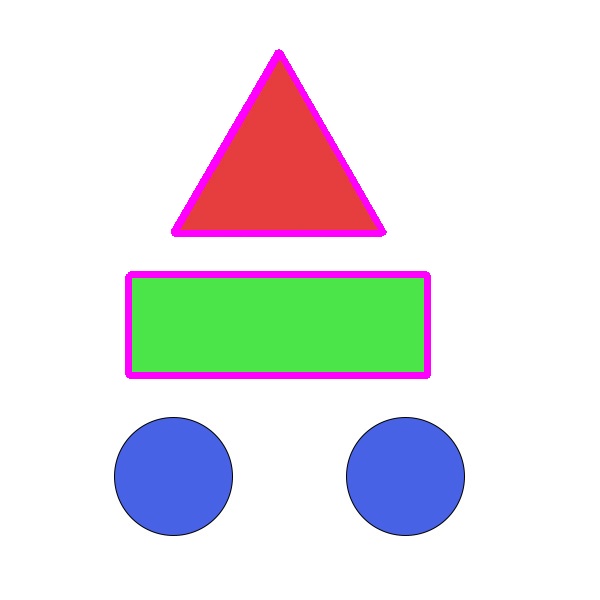
2、输入带有已知几何形状的图像,实现HOUGH变换检测直线,并定位几何图形
霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。
在这个问题中,hough变换能够检测出直线或者直线段,但是想要定位三角形矩形之类的,就需要对原图像要求比较纯净,否则应该需要配合其他手段进行检测。这里的主要思路是将图片灰度化之后,进行二值化,然后在使用canny进行边缘检测,然后对处理之后的图像应用hough变换而来。这里使用的是open cv检测直线段的函数,需要自定义最小线段的长度。
| origin | processed |
|---|---|
 |
 |
 |
 |
 |
 |
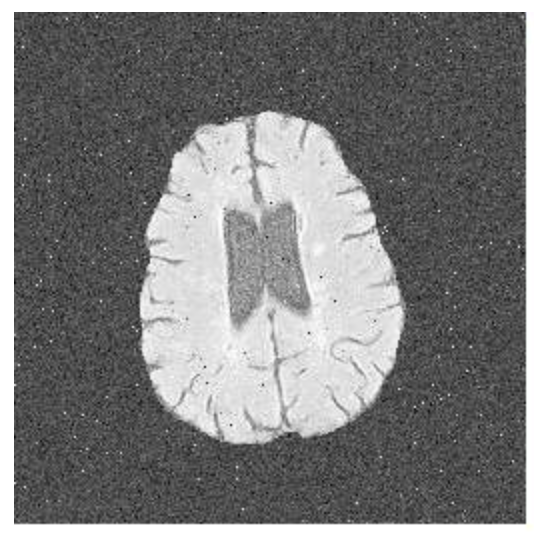
3、采用大津法实现二值化;实现动态阈值分割
大津法(OTSU)是一种确定图像二值化分割阈值的算法。对于图像,前景(即目标)和背景的分割阈值记作,属于前景的像素点数占整幅图像的比例记为,其平均灰度;背景像素点数占整幅图像的比例为,其平均灰度为。图像的总平均灰度记为,类间方差记为g。假设图像的背景较暗,并且图像的大小为,图像中像素的灰度值小于阈值的像素个数记作,像素灰度大于阈值的像素个数记作,则有:
ω_0=N_0/ M×N \tag{5}$$ $$ω_1=N_1/ M×N \tag{6} $$ $$N_0+N_1=M×N \tag{7} $$ $$ω_0+ω_1=1 \tag{8} $$ $$μ=ω_0*μ_0+ω_1*μ_1\tag{9} $$ $$g=ω_0(μ_0-μ)^2+ω_1(μ_1-μ)^2 \tag{10}将式(9)代入式(10),得到等价公式,也就是类间方差: $$g=ω_0ω_1(μ_0-μ1_)^2 \tag{11}$$采用遍历的方法得到使类间方差最大的阈值,即为所求。
动态阈值分割的原理是计算局部区域的平均值,中位数,高斯加权平均值,以确定遍历图像所有区域的阈值,这里使用的是opencv的库。
| origin | otsu | dynamic |
|---|---|---|
 |
 |
 |
 |
 |
 |
可以发现,在第一行的图中,原图的亮度分布比较均匀,因此大津法这种计算全局阈值的算法也可以有很好的效果。而在第二行的图中,原图的亮度分布不均匀,大津法计算全局阈值的算法并不能很好地处理这个问题,在光线较暗的地方,会被处理成背景黑色。而动态阈值则能很好地解决这个问题。
4、实现基于数学形态学的纹理分割
基于数学形态学的纹理分割可以将半径不同的图像区分开来。比如,对于一个图像中有半径不同的两种黑色圆,想要找一个分界线将两者分开,就可以使用基于数学形态学的纹理分割。
首先,使用形态闭操作去消灭小圆,形态闭操作实际上是由膨胀和腐蚀组合而成。通过选择一个比小圆半径大大圆半径小的一个值,使得小圆在膨胀过程中消失。
然后,使用形态开操作去使得大圆的区域变成一整块黑色区域,形态开操作实际上是由腐蚀和膨胀组合而成,通过选择一个比大圆半径还大的值,使得大圆在腐蚀的过程中消失。
之后,我使用的是canny边缘检测,去检测图像的边缘。最后将原图和边缘叠加起来,就实现了区分的效果。
| origin | after1 | after2 | after3 | after4 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
三、大作业
1、Graph cut
Graph cuts是一种十分有用和流行的能量优化算法,在计算机视觉领域普遍应用于前背景分割(Image segmentation)、立体视觉(stereo vision)、抠图(Image matting)等。此类方法把图像分割问题与图的最小割(min cut)问题相关联。假设图像的分割为时,图像的能量可以表示为:
其中,为区域项(regional term),为边界项(boundary term),而就是区域项和边界项之间的重要因子
另外由于Graph Cuts需要有2个终端节点”S”和”T”,分别表示初始的目标区域和背景区域。在实际操作中,使用鼠标给定目标区域和背景区域,作为这两个区域像素分布的先验。有了能量函数的定义和初始的终端顶点,就可以采用图割理论来不断迭代对目标进行分割了。
实验结果如下:
| origin | processed |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
GraphCut优缺点分析:
优点:一次迭代,计算速度快
缺点:需要人工标注,消耗时间,人机交互不友好,迭代一次不能进行优化,使用灰度直方图来计算彩色像素的概率,会有误差。
2、SLIC超像素分割
超像素概念是2003年Xiaofeng Ren提出和发展起来的图像分割技术,是指具有相似纹理、颜色、亮度等特征的相邻像素构成的有一定视觉意义的不规则像素块。这里使用的是SLIC(simple linear iterativeclustering),即简单的线性迭代聚类。它是2010年提出的一种思想简单、实现方便的算法,将彩色图像转化为CIELAB颜色空间和XY坐标下的5维特征向量,然后对5维特征向量构造距离度量标准,对图像像素进行局部聚类的过程。
基本流程如下:
- 初始化种子点(聚类中心)
- 在种子点的n*n邻域内重新选择种子点
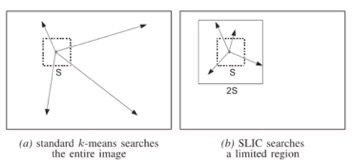
- 在每个种子点周围的邻域内为每个像素点分配类标签
- 距离度量。包括颜色距离和空间距离
- 迭代优化
实验结果如下:
- 观察迭代次数对于实验结果的影响
迭代次数1次,6次,10次进行实验(K=50,M=40)
| iteraion 1 | iteration 6 | iteration 10 |
|---|---|---|
 |
 |
 |
| iteraion 1 | iteration 6 | iteration 10 |
|---|---|---|
 |
 |
 |
可以发现,迭代次数越高,超像素分割的块更加整齐。
- 观察K的大小对于实验结果的影响:
分别对K=50,100,200进行实验 (M=40,迭代10次)
| K = 50 | K = 100 | K = 200 |
|---|---|---|
 |
 |
 |
| K = 50 | K = 100 | K = 200 |
|---|---|---|
 |
 |
 |
K影响的是分块个数,K有几个,分块就有几块。
- 观察M的大小对于实验结果的影响:
分别对M=10,20,40进行实验 (K=50,迭代10次)
| M = 10 | M = 20 | M = 40 |
|---|---|---|
 |
 |
 |
| M = 10 | M = 20 | M = 40 |
|---|---|---|
 |
 |
 |
M是用于平衡像素空间距离和像素值的权重。M的大小会影响分块的工整性。M越大,分块越工整。
大作业所使用的数据集均来自于https://pjreddie.com/projects/pascal-voc-dataset-mirror/中VOC2007。



